7 Days0Site 7 Days0
30 Days0Site 30 Days0
Total0Site Total0

Quantum Mechanics Note

Date: 2024/05/27
Last Updated: 2024-05-28T12:49:25.000Z
Categories: Physics
Tags: Physics, Quantum Mechanics
Read Time: 12 minutes

0.1 Contents

0.2 Probability Basics

0.2.1 Random Variable

A random variable X is a function that maps the sample space \Omega to the real number line \mathbb{R}.

0.2.2 Probability Density Function

The probability density function f(x) of a random variable X is a function that describes the likelihood of the random variable to take on a specific value.

0.2.3 Cumulative Distribution Function

The cumulative distribution function F(x) of a random variable X is a function that describes the probability that the random variable takes on a value less than or equal to x.

F(x) = P(X \leq x) = \int_{-\infty}^x f(x) dx.

0.2.4 Expectation

The expectation of a random variable X is the average value of the random variable.

<X> = \int_{-\infty}^{\infty} x f(x) dx.

0.2.5 Variance

The variance of a random variable X is a measure of how much the values of the random variable vary.

\Delta X^2 = <(X - <X>)^2> = <X^2> - <X>^2.

0.2.6 Standard Deviation

The standard deviation of a random variable X is the square root of the variance.

\Delta X = \sqrt{\Delta X^2}.

0.2.7 Probability Amplitude

The probability amplitude \psi(x) of a random variable X is a complex value function that the likelihood of the random variable to take on value x is given by |\psi(x)|^2.

In other words, the probability density function f(x) is given by

f(x) = |\psi(x)|^2.

0.3 Calculus Basics

0.3.1 Gaussian Integral

The Gaussian integral is given by

\int_{-\infty}^{\infty} e^{-\frac{x^2}{\sigma^2}} dx = \sqrt{\pi}\sigma.

0.3.1.1 Odd Powers of x in Gaussian Integral

The Gaussian integral with odd powers of x is given by

\int_{-\infty}^{\infty} x^{2n+1} e^{-\frac{x^2}{\sigma^2}} dx = 0.

As this is an odd function, the integral is zero.

0.3.1.2 Even Powers of x in Gaussian Integral

The even powers of x in Gaussian integral can be calculated using Feynman's trick.

\begin{align} \int_{-\infty}^{\infty} x^{2n} e^{-ax^2} dx &= \int_{-\infty}^{\infty} \left(-\frac{\partial}{\partial a}\right)^n e^{-ax^2} \\ &= \left(-\frac{\partial}{\partial a}\right)^n \int_{-\infty}^{\infty} e^{-ax^2} dx \\ &= \left(-\frac{\partial}{\partial a}\right)^n \sqrt{\frac{\pi}{a}} \end{align}

0.4 Wave Function

We can postulate that the state of a particle is described by a complex value wave function \Psi(x, t), where x is the position and t is the time.

0.4.1 Born Rule

The probability density to find the particle at position x is given by |\Psi(x, t)|^2. And thus, the probability to find the particle in an measurable area A is given by

P(A) = \int_A |\Psi(x, t)|^2 dx.

0.4.2 Continuity Requirement of Wave Function

The wave function \Psi(x, t) must be continuous and differentiable.

0.4.3 Normalizing Wave Function

The wave function \Psi(x, t) defined on space X is normalized if

\int_{X} |\Psi(x, t)|^2 dx = 1.

If the wave function is not normalized, and if A=\int_{X} |\Psi(x, t)|^2 dx is finite and greater than 0, then the normalized wave function is given by

\Psi_{\text{normalized}}(x, t) = \frac{\Psi(x, t)}{\sqrt{A}}.

0.4.4 Superposition Principle of Wave Functions

If \Psi_1(x, t) and \Psi_2(x, t) are two wave functions, then the superposition of the wave functions is given by

\Psi(x, t) = c_1 \Psi_1(x, t) + c_2 \Psi_2(x, t),

where c_1 and c_2 are complex numbers. And \Psi is also a wave function.

0.4.5 Interference of Wave Functions

The interference of wave functions is a phenomenon where two wave functions \Psi_1(x, t) and \Psi_2(x, t) interfere with each other to form a new wave function \Psi(x, t).

Let \Psi(x, t) = \Psi_1(x, t) + \Psi_2(x, t). Then the probability density of the new wave function is given by

|\Psi(x, t)|^2 = |\Psi_1(x, t)|^2 + |\Psi_2(x, t)|^2 + \Psi_1(x, t)^* \Psi_2(x, t) + \Psi_1(x, t) \Psi_2(x, t)^*

And the \Psi_1(x, t)^* \Psi_2(x, t) + \Psi_1(x, t) \Psi_2(x, t)^* is usually called the interference term.

0.4.6 Classical Plane Wave

The classical plane wave is given by

\Psi(x, t) = A e^{ikx - i\omega t}

where A is the amplitude, k is the wave number, and \omega is the angular frequency.

Note: The classical plane wave is not normalizable, as the integral of the probability density is infinite. In this case, we can use \Psi(x, t) = A e^{ikx - i\omega t -iax^2} where a is a relatively small positive constant. The new wave function is normalizable and have similar behaviour to the plane wave near the origin.

0.5 Schrödinger Equation

0.5.1 Reduced Planck Constant

The reduced Planck constant is given by

\hbar = \frac{h}{2\pi} \approx 1.0545718 \times 10^{-34} \text{ J s}.

where h is the Planck constant.

0.5.2 Quantization Rule

The quantization rule is given by

\begin{align} \hat{p} &= -i \hbar \nabla \\ \hat{E} &= i \hbar \frac{\partial}{\partial t} \end{align}

0.5.3 Schrödinger Equation for Free Particle

In classical mechanics, the energy of a free particle is given by

E = T + V = \frac{p^2}{2m} + V(x).

By applying the quantization rule, the Schrödinger equation (SE) for a free particle with wave equation \psi is given by

\begin{align} \hat{E}\psi &= \left[\frac{\hat{p}^2}{2m} + V\right]\psi \\ i \hbar \frac{\partial \psi}{\partial t} &= \left[-\frac{\hbar^2}{2m} \nabla^2 + V\right]\psi = \left[-\frac{\hbar^2}{2m} \Delta + V\right]\psi \end{align}

0.5.4 Hamiltonian Operator

The Hamiltonian operator \hat{H} is given by

\hat{H} = \frac{\hat{p}^2}{2m} + V(x)

Using the Hamiltonian operator, the Schrödinger equation for a free particle is given by

\hat{E} \frac{\partial \psi}{\partial t} = \hat{H}\psi.

0.5.5 Using Separation of Variables to Solve Schrödinger Equation

The Schrödinger equation can be solved using separation of variables. Let \psi(x, t) = \phi(x) \tau(t). Then the Schrödinger equation becomes

\begin{align} \hat{E}\psi &= \hat{H}\psi \\ \phi \hat{E} \tau &= \tau \hat{H} \phi \\ \frac{\hat{E} \tau}{\tau} &= \frac{\hat{H} \phi}{\phi} = E \\ i\hbar \frac{\partial}{\partial t} \tau &= E \tau \\ \tau &= e^{-iEt/\hbar} \\ \hat{H} \phi &= E \phi \end{align}

Assume, \phi_1,\phi_2,\ldots solve \hat{H} \phi = E \phi with E_1,E_2,\ldots. Then the general solution is given by

\phi(x) = \sum_{n=1}^{\infty} c_n \phi_n(x)e^{-iE_nt/\hbar}.

0.5.6 Time-Independent Schrödinger Equation

By the previous discussion, the task of solving the Schrödinger equation is reduced to solving the equation

\hat{H} \phi_n = E_n \phi_n.

This equation is called the time-independent Schrödinger equation (TISE).

We always call E_n eigenvalues of H. And it is also known as:

  1. Energy lLevels
  2. Eigenenergies
  3. Energy Eigenvalues

And \phi_n are called energy eigenstates of H. And it is also known as:

  1. Stationary States
  2. Energy Eigenfunctions

0.5.6.1 Degeneracy of TISE Solutions

If two or more energy eigenstates have the same energy eigenvalue, then the energy eigenvalue is said to be degenerate.

If two eigenstates have the same eigenvalue, we call it degeneracy of order 2 or twice degenerate.

0.6 Double Slit Experiment

Consider the following double slit experiment setup.

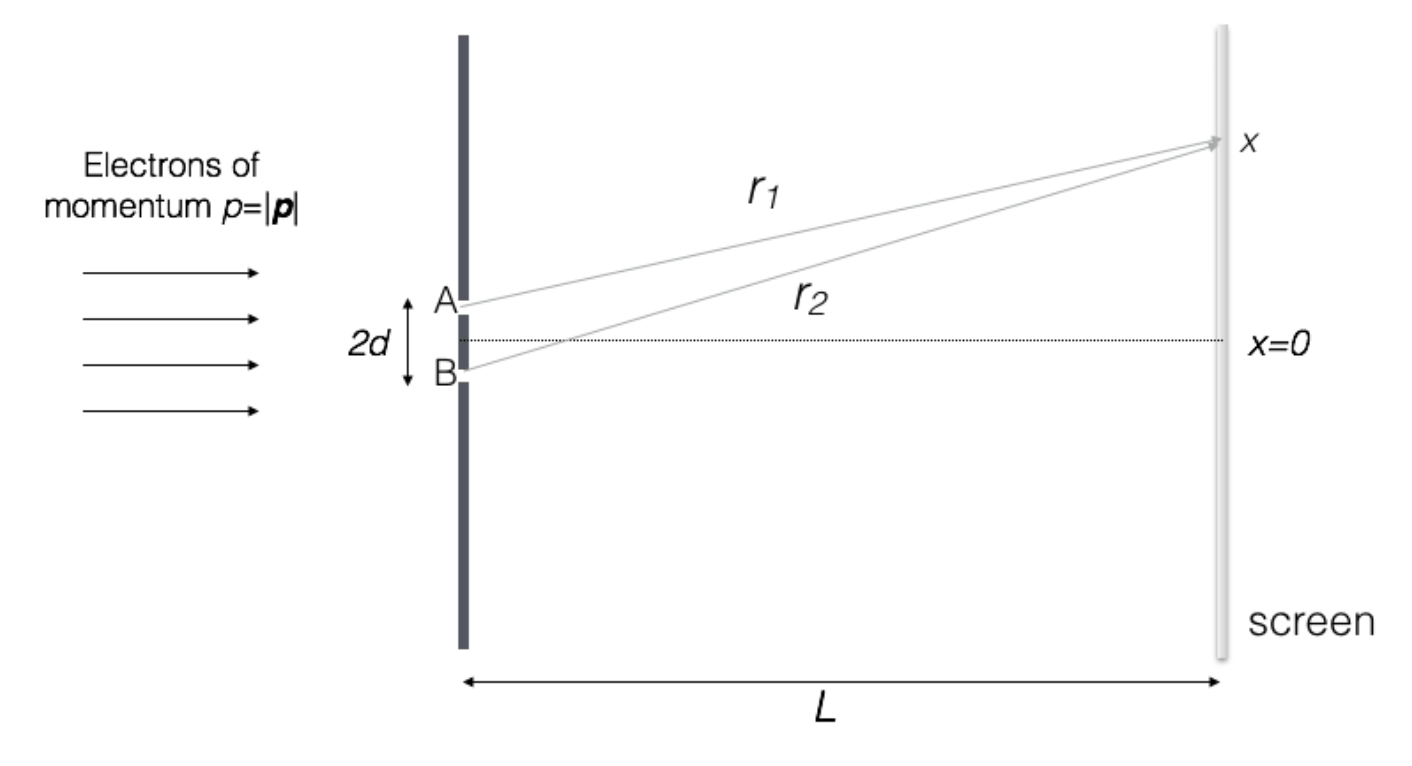
Double Slit Experiment

We can assume the wave function that go through the slits A and B are the same, and is given by the analogue of plane wave \psi(r, t) = \frac{e^{ikx-iwt}}{r}.

Then, for any point P on the screen, the wave function is the superposition of the wave functions from the slits A and B.

\begin{align} \Psi(x, t) &= \psi_A(r_1, t) + \psi_B(r_2, t) \\ &= e^{ikr_1-iwt} + e^{ikr_2-iwt} \\ &= e^{-iwt}\left[\frac{e^{ikr_1}}{r_1} + \frac{e^{ikr_2}}{r_2}\right] \end{align}

where r_1 and r_2 are the distances from the slits A and B to the point P. And is given by

\begin{align} r_1 &= \sqrt{L^2 + (x-d)^2} \\ r_2 &= \sqrt{L^2 + (x+d)^2} \end{align}

Without normalization, the probability density of the wave function is proportional to

\begin{align} |\Psi(x, t)|^2 &= \left|\frac{e^{ikr_1}}{r_1} + \frac{e^{ikr_2}}{r_2}\right|^2 \\ &= \frac{1}{r_1^2} + \frac{1}{r_2^2} + \frac{1}{r_1r_2}\left[e^{ik(r_1-r_2)} + e^{-ik(r_1-r_2)}\right] \\ &\approx \frac{1}{L^2}\left[2 + 2\cos(k(r_1-r_2))\right] \\ &= \frac{1}{L^2}\left[2 + 2\cos\left( k \left( \sqrt{L^2 + (x+d)^2} - \sqrt{L^2 + (x-d)^2} \right) \right) \right] \\ &= \frac{1}{L^2}\left[2 + 2\cos\left( k \frac{ 4dx }{ \sqrt{L^2 + (x+d)^2} + \sqrt{L^2 + (x-d)^2} } \right) \right] \\ &\approx \frac{1}{L^2}\left[2 + 2\cos\left( k \frac{ 4dx }{ 2L } \right)\right] \quad\text{As } L \gg x,d \\ &= \frac{1}{L^2}\left[2 + 2\cos\left( k \frac{ 2dx }{ L } \right)\right] \end{align}

We can see that the probability density of the wave function is proportional to a transformed cosine function, which explains the interference pattern on the screen.

0.7 Parity of TISE Solutions

0.7.1 Even potential and Parity

Given a potential V(x): \mathbb{R}\rightarrow \mathbb{C}, the potential is said to be even if

V(x) = V(-x)

In such cases, we can assume the TISE solution has definite parity, that is:

\phi(x) = \pm \phi(-x)

0.7.2 Real Potential and Parity

Given a real potential V(x), we can assume the TISE solution to have definite parity regarding conjugation, that is:

\phi(x) = \phi^*(x)

0.8 States of TISE Solutions

In general there are three kinds of states of TISE solutions:

  1. Bound States
  2. Scattering States
  3. Non-physical States

0.8.1 Bound States

Bound states are states where the energy eigenvalue E_n is less than the potential energy at infinity and greater than the minimum potential energy. In such cases, the TISE solution is normalizable, and the energy eigenvalue is quantized.

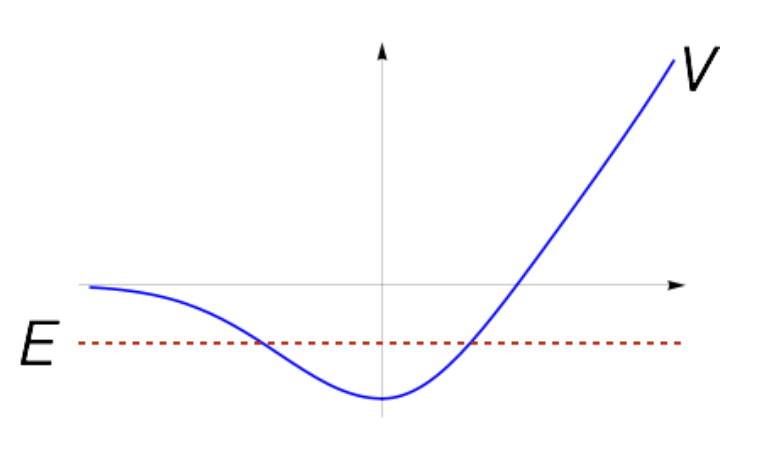
Bound States

0.8.2 Scattering States

Scattering states are states where the energy eigenvalue E_n is greater than the potential energy at infinity. In such cases, the TISE solution is not normalizable, and the energy eigenvalue is continuous.

Scattering states can be approximated by normalizable states by similar method as the classical plane wave.

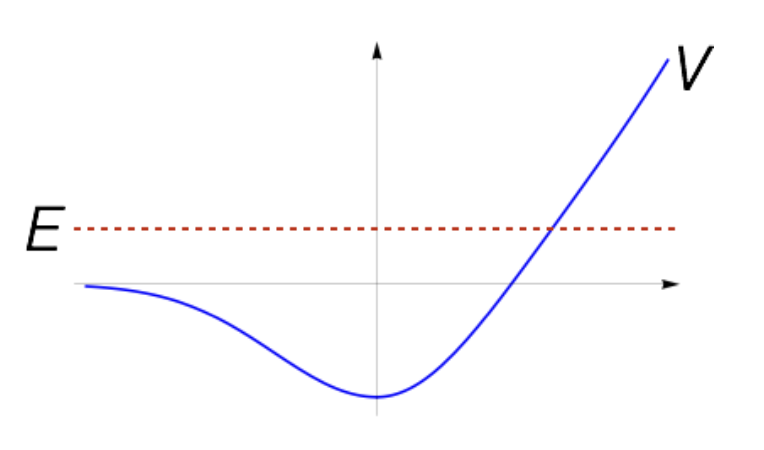
Scattering States

0.8.3 Non-physical States

Non-physical states are states where the energy eigenvalue E_n is less than the minimum potential energy. This case cannot happen in real physical systems.

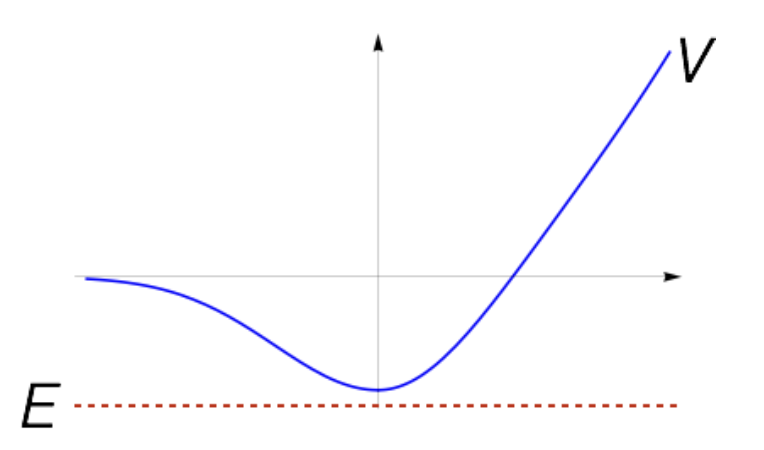
Non-physical States

0.9 Continuity Equation and Probability Current

Consider the potential to be real. Define the probability density of a wave function P = \Psi(x, t) as |\Psi(x, t)|^2. Then:

\begin{align} \frac{\partial}{\partial t} P &= \frac{\partial \psi}{\partial t} \psi^* + \psi \frac{\partial \psi}{\partial t}^* \\ &= \frac{1}{i\hbar}\left[ \hat{H}\psi\psi^* - \psi(\hat{H}\psi)^* \right] \\ &= -\frac{\hbar^2}{i\hbar 2m}\left[ \frac{\partial^2 \psi}{\partial x^2}\psi^* - \psi\frac{\partial^2 \psi}{\partial x^2}^* \right] \\ &= -\frac{d}{dx}\left[\frac{\hbar^2}{i\hbar 2m}\left[ \frac{\partial \psi}{\partial x}\psi^* - \frac{\partial \psi}{\partial x}\frac{\partial \psi}{\partial x}^* - \psi\frac{\partial \psi}{\partial x}^* + \frac{\partial \psi}{\partial x}\frac{\partial \psi}{\partial x}^* \right]\right] \\ &= -\frac{d}{dx}\left[\frac{\hbar}{2mi}\left[ -\psi\frac{\partial \psi}{\partial x}^* + \psi^*\frac{\partial \psi}{\partial x} \right]\right] \end{align}

We thus define the probability current J as

J = \frac{\hbar}{2mi}\left[ -\psi\frac{\partial \psi}{\partial x}^* + \psi^*\frac{\partial \psi}{\partial x} \right]

The above equation become:

\frac{\partial P}{\partial t} = -\frac{dJ}{dx}

and is called the continuity equation.

0.10 Quantum Tunnelling

We consider a potential barrier of height V_0 and width 2a.

That is, the potential is given by

V(x) = \begin{cases} V_0 & \text{if } |x| < 2a \\ 0 & \text{otherwise} \end{cases}

Then, the TISE can be divided into three regions:

  1. Region I: x < -a
\frac{d^2 \psi}{dx^2} = -\frac{2m}{\hbar^2}E\psi
  1. Region II: -a < x < a
\frac{d^2 \psi}{dx^2} = -\frac{2m}{\hbar^2}(E-V_0)\psi
  1. Region III: x > a
\frac{d^2 \psi}{dx^2} = -\frac{2m}{\hbar^2}E\psi

0.10.1 Simplified Model of Quantum Tunnelling

For the sake of simplicity, let k = \sqrt{\frac{2mE}{\hbar^2}} we can assume the solution of the TISE in Region I and Region III to be

In region I:

\psi(x) = A e^{ikx} + B e^{-ikx}

In region III:

\psi(x) = F e^{ikx}

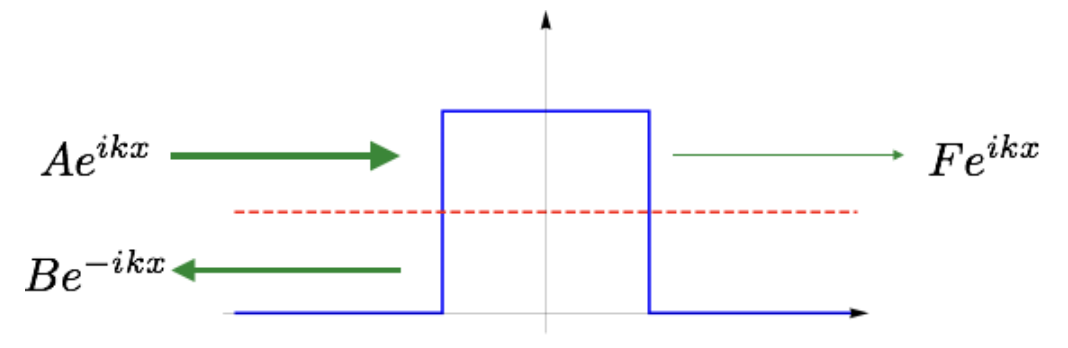
Quantum Tunnelling

The wave A e^{ikx} can be interpreted as the wave go toward the barrier, and the wave B e^{-ikx} can be interpreted as the wave being reflected by the barrier and wave F e^{ikx} can be interpreted as the wave go through the barrier.

As there is no probability for the particle to be in region II, the probability current must be same at the point x = a and x = -a.

In region I:

J = \frac{\hbar}{2mi}\left[ \psi\frac{-\partial \psi}{\partial x}^* + \psi^*\frac{\partial \psi}{\partial x} \right] = \frac{\hbar k}{m}(|A|^2 - |B|^2)

In region III:

J = \frac{\hbar}{2mi}\left[ \psi\frac{-\partial \psi}{\partial x}^* + \psi^*\frac{\partial \psi}{\partial x} \right] = \frac{\hbar k}{m}|F|^2

Thus, we have

|A|^2 - |B|^2 = |F|^2

We define the reflection probability R and transmission probability T as

\begin{align} R &= \frac{|B|^2}{|A|^2} \\ T &= \frac{|F|^2}{|A|^2} \end{align}

Then, we have

R + T = 1

0.10.2 Quantum Tunnelling through High and Thin Barrier

We consider a barrier that is infinitely high and thin at origin.

To state this formally, we consider the potential to be the limiting behaviour of the Dirac delta function potential.

\delta_L(x) = \begin{cases} \frac{1}{L} & \text{if } -\frac{L}{2} < x < \frac{L}{2} \\ 0 & \text{otherwise} \end{cases}

and

\delta = \lim_{L \to 0} \delta_L(x)

Also, for all function g(x), we have

\lim_{\epsilon \to 0} \int_{-\epsilon}^{\epsilon} g(x) \delta(x) dx = g(0)

Then, the potential is given by

V(x) = \alpha \delta(x)

We again, consider the simplified model in the previous section.

In region I:

\psi(x) = A e^{ikx} + B e^{-ikx}

In region III:

\psi(x) = F e^{ikx}

As the region II is infinity thin, the right hand side of the region I and the left hand side of the region III must be the same.

Thus, we have

A + B = F

Also, by integrating the TISE over the region [-\epsilon,\epsilon], we get:

\begin{align} \int_{-\epsilon}^{\epsilon} \frac{d^2 \psi}{dx^2} dx &= -\frac{2m}{\hbar^2} \int_{-\epsilon}^{\epsilon} (E-\alpha\delta(x))\psi dx \\ \left[\frac{d \psi}{dx}\right]_{-\epsilon}^{\epsilon} &= -\frac{2m}{\hbar^2} \left[E\psi(\epsilon)-E\psi(-\epsilon) - \alpha\int_{-\epsilon}^{\epsilon} \psi\delta dx\right] \\ \end{align}

Taking the limit \epsilon \to 0, we get

\begin{align} \left[\frac{d \psi}{dx}\right]_{0^+} - \left[\frac{d \psi}{dx}\right]_{0^-} &= \frac{2m}{\hbar^2} \alpha \psi(0) \end{align}

Substituting the solution of the TISE in region I and region III, we get

ik(A-B) - ikF = \frac{2m}{\hbar^2} \alpha F

Solving the above equation, we can get the reflection and transmission probability.

0.11 Functional Analysis of Quantum Mechanics

0.11.1 Hilbert Space

Define the Hilbert space \mathbf{H} as the space of all possible wave functions \Psi(x, t) that are square integrable.

\mathbf{H} = \left\{ \Psi(x, t) \mid \int_{-\infty}^{\infty} |\Psi(x, t)|^2 dx < \infty \right\}

The Hilbert space is a complex vector space.

0.11.2 Inner Product

We define the inner product of two wave functions \Psi_1(x, t) and \Psi_2(x, t) as

\left<\Psi_1, \Psi_2\right> = \int_{-\infty}^{\infty} \Psi_1^*(x, t) \Psi_2(x, t) dx

0.11.2.1 Properties of Inner Product

  1. Linearity in Second Argument: For all \Psi_1, \Psi_2 \in \mathbf{H} and a,b \in \mathbb{C}, we have \left<a\Psi_1 + b\Psi_2, \Psi_3\right> = a\left<\Psi_1, \Psi_3\right> + b\left<\Psi_2, \Psi_3\right>.
  2. Anti-linearity in First Argument: For all \Psi_1, \Psi_2 \in \mathbf{H} and a,b \in \mathbb{C}, we have \left<\Psi_1, a\Psi_2 + b\Psi_3\right> = a^*\left<\Psi_1, \Psi_2\right> + b^*\left<\Psi_1, \Psi_3\right>.
  3. Positive Definite: For all \Psi \in \mathbf{H}, we have \left<\Psi, \Psi\right> \geq 0 and \left<\Psi, \Psi\right> = 0 if and only if \Psi = 0.
  4. Conjugate Symmetric (Skew Symmetric): For all \Psi_1, \Psi_2 \in \mathbf{H}, we have \left<\Psi_1, \Psi_2\right> = \left<\Psi_2, \Psi_1\right>^*.

0.11.3 Norm

The norm of a wave function \Psi(x, t) is defined as

||\Psi|| = \sqrt{\left<\Psi, \Psi\right>}

0.11.4 Orthogonality

Two wave functions \Psi_1(x, t) and \Psi_2(x, t) are said to be orthogonal if

\left<\Psi_1, \Psi_2\right> = 0

0.11.5 Angle

The angle between two wave functions \Psi_1(x, t) and \Psi_2(x, t) is defined as

\cos\theta = \frac{\left<\Psi_1, \Psi_2\right>}{||\Psi_1|| ||\Psi_2||}

0.11.6 Orthonormal Basis

A set of wave functions \{\Psi_1(x, t), \Psi_2(x, t), \ldots\} is said to be an orthonormal basis if

  1. The set is orthogonal.
  2. The set is normalized.
  3. The set spans the Hilbert space. That is, for all \Psi(x, t) \in \mathbf{H}, there exists a set of complex numbers \{c_1, c_2, \ldots\} such that
\Psi(x, t) = \sum_{n=1}^{\infty} c_n \Psi_n(x, t)

0.11.7 Operator

An operator is a function that maps a wave function to another wave function.

0.11.8 Hermitian Conjugate

The Hermitian conjugate of an operator \hat{A} is denoted by \hat{A}^\dagger and is the unique operator that satisfies

\left<\hat{A}\Psi_1, \Psi_2\right> = \left<\Psi_1, \hat{A}^\dagger\Psi_2\right>

0.11.9 Hermitian Operator

An Hermitian operator is an operator that satisfies

\left<\hat{A}\Psi_1, \Psi_2\right> = \left<\Psi_1, \hat{A}\Psi_2\right>

for all \Psi_1, \Psi_2 \in \mathbf{H}.

An equivalent definition is that the operator is equal to its Hermitian conjugate.

0.11.10 Spectral Theorem

The spectral theorem states that for all Hermitian operators \hat{A}, there exists an orthonormal basis \{\Psi_1(x, t), \Psi_2(x, t), \ldots\} such that

\hat{A}\Psi_n(x, t) = a_n\Psi_n(x, t)

where a_n are the eigenvalues of \hat{A} and is real.

0.11.10.1 Hamiltonian Operator is Hermitian

The Hamiltonian operator \hat{H} is Hermitian.

Proof:

\begin{align} \left<\hat{H}\Psi_1, \Psi_2\right> &= \int_{-\infty}^{\infty} \Psi_1^*(x, t) \hat{H}\Psi_2(x, t) dx \\ &= \int_{-\infty}^{\infty} \Psi_1^*(x, t) \left[-\frac{\hbar^2}{2m}\frac{\partial^2 \Psi_2}{\partial x^2} + V(x)\Psi_2(x, t)\right] dx \quad \text{By Integration By Part} \\ &= \int_{-\infty}^{\infty} \left[-\frac{\hbar^2}{2m}\frac{\partial^2 \Psi_1^*}{\partial x^2} + V(x)\Psi_1^*(x, t)\right] \Psi_2(x, t) dx \\ &= \left<\Psi_1, \hat{H}\Psi_2\right> \end{align}

0.11.11 Positivity Operators

An operator \hat{A} is said to be positive definite if give any non-zero wave function \Psi(x, t), we have

\left<\hat{A}\Psi, \Psi\right> > 0

An operator \hat{A} is said to be positive semi-definite if give any wave function \Psi(x, t), we have

\left<\hat{A}\Psi, \Psi\right> \geq 0

Any operator given by \hat{A} = \hat{B}^\dagger \hat{B} is positive semi-definite.

0.12 Measurement Postulate

Given a orthonormal basis \{\Psi_1(x, t), \Psi_2(x, t), \ldots\}, the measurement postulate states that the probability of measuring the normalized wave function \Psi(x, t) to be in the state \Psi_n(x, t) is given by

P_n = \left|\left<\Psi_n, \Psi\right>\right|^2

0.12.1 Post Measurement State

After the measurement, the state of the wave function will collapse to the state that is measured.

0.13 Measurement of Observables

Given an observable \hat{A}, it is postulated that \hat{A} is Hermitian and has an orthonormal basis \{\Psi_1(x, t), \Psi_2(x, t), \ldots\}.

The expectation value of the observable \hat{A} of a wave function \psi is given by

\left<\hat{A}\right> = \sum_{n=1}^{\infty} a_n P_n = \left<\psi|\hat{A}\psi\right>

0.14 Commutators and Lie Bracket

In general, two operators \hat{A} and \hat{B} do not commute.

We define the commutator (Lie Bracket) of two operators \hat{A} and \hat{B} as

[\hat{A}, \hat{B}] = \hat{A}\hat{B} - \hat{B}\hat{A}

0.14.1 Properties of Commutators

  1. Linearity: [a\hat{A} + b\hat{B}, \hat{C}] = a[\hat{A}, \hat{C}] + b[\hat{B}, \hat{C}]
  2. Anti-linearity: [\hat{A}, a\hat{B} + b\hat{C}] = a[\hat{A}, \hat{B}] + b[\hat{A}, \hat{C}]
  3. Linearity in Second Argument: [\hat{C}, a\hat{A} + b\hat{B}] = a[\hat{C},\hat{A}] + b[\hat{C},\hat{B}]
  4. Distributivity: [\hat{A}, \hat{B}\hat{C}] = [\hat{A}, \hat{B}]\hat{C} + \hat{B}[\hat{A}, \hat{C}]

0.14.1.1 Commutator of Position and Momentum Operators

The commutator of position operator \hat{x} and momentum operator \hat{p} is given by

\begin{align} [\hat{x},\hat{p}] &= \hat{x}\hat{p} - \hat{p}\hat{x} \\ &= x\left(-i\hbar\frac{\partial}{\partial x}\right) - \left(-i\hbar\frac{\partial}{\partial x}\right)x \\ &= x\left(-i\hbar\frac{\partial}{\partial x}\right) - \left(-i\hbar\right) - x\left(-i\hbar\frac{\partial}{\partial x}\right) \\ &= i\hbar \end{align}

0.15 Compatibility of Observables

Two observables \hat{A} and \hat{B} are said to be compatible if they commute.

0.16 Robertson Inequality

The Robertson Inequality states that for any two observables \hat{A} and \hat{B}, we have

\Delta \hat{A} \Delta \hat{B} \ge \frac{1}{2} \left|\left<[\hat{A}, \hat{B}]\right>\right|

Proof:

Without loss of generality, we can assume \left<\hat{A}\right> = 0 and \left<\hat{B}\right> = 0. Otherwise we replace \hat{A} with \hat{A} - \left<\hat{A}\right> and \hat{B} with \hat{B} - \left<\hat{B}\right>.

Then, we have

\begin{align} \Delta \hat{A} \Delta \hat{B} &= \sqrt{\left<\hat{A}^2\right>\left<\hat{B}^2\right>} \\ &= \sqrt{\left<\hat{A}\psi|\hat{A}\psi\right>\left<\hat{B}\psi|\hat{B}\psi\right>} \\ &\ge \left|\left<\hat{A}\psi|\hat{B}\psi\right>\right| \quad \text{Cauchy-Schwartz}\\ &= \left|\left<\psi|\hat{A}\hat{B}\psi\right>\right| \\ \end{align}

By similar argument, we have

\Delta \hat{A} \Delta \hat{B} \ge \left|\left<\psi|\hat{B}\hat{A}\psi\right>\right|

Thus,

\begin{align} \Delta \hat{A} \Delta \hat{B} &= \frac{1}{2}\left(\Delta \hat{A} \Delta \hat{B} + \Delta \hat{A} \Delta \hat{B}\right) \\ &\ge \frac{1}{2}\left( \left|\left<\psi|\hat{A}\hat{B}\psi\right>\right| + \left|\left<\psi|\hat{B}\hat{A}\psi\right>\right| \right)\\ &\ge \frac{1}{2}\left| \left<\psi|\hat{A}\hat{B}\psi\right> - \left<\psi|\hat{B}\hat{A}\psi\right> \right| \\ &= \frac{1}{2}\left| \left<\psi|[\hat{A}, \hat{B}]\psi\right> \right| \\ \end{align}

0.16.1 Robertson Inequality for Position and Momentum Operators

Given the position operator \hat{x} and momentum operator \hat{p}, we have

\Delta \hat{x} \Delta \hat{p} \ge \frac{\hbar}{2}

0.17 Quantum Harmonic Oscillator

A quantum harmonic oscillator is a system where the potential energy is given by

V(x) = \frac{1}{2}m\omega^2x^2

0.17.1 Annihilation and Creation Operators

Given the Hamiltonian operator \hat{H} of the quantum harmonic oscillator, we can define the annihilation operator \hat{a} and creation operator \hat{a}^\dagger as

\begin{align} \hat{a} &= u\hat{x} + v\hat{p} i \\ \hat{a}^\dagger &= u\hat{x} - v\hat{p} i \end{align}

Thus, we have

\begin{align} \hat{a}\hat{a}^\dagger &= u^2 \hat{x}^2 - v^2 \hat{p}^2 - uv \hat{x}\hat{p} i + uv \hat{p}\hat{x} i \\ &= u^2 \hat{x}^2 - v^2 \hat{p}^2 + uv\hbar \\ \end{align}

If we take:

\begin{align} u^2 &= \frac{1}{2\hbar}m\omega \\ v^2 &= \frac{1}{2 m\omega\hbar} \\ \end{align}

Then, we have

\begin{align} \hat{a}\hat{a}^\dagger &= \frac{1}{2\hbar}m\omega \hat{x}^2 + \frac{1}{2 m\omega\hbar} \hat{p}^2 + \frac{1}{2} \\ &= \frac{1}{\hbar\omega}\hat{H} + \frac{1}{2} \end{align}

0.17.2 Bosonic Commutation Relation

Given the annihilation operator \hat{a} and creation operator \hat{a}^\dagger of the quantum harmonic oscillator, we have

[\hat{a}, \hat{a}^\dagger] = 2uvh = 1

0.17.3 Number Operator

Given the annihilation operator \hat{a} and creation operator \hat{a}^\dagger of the quantum harmonic oscillator, we can define the number operator \hat{N} as

\hat{N} = \hat{a}^\dagger\hat{a}

Thus, we have

\begin{align} \hat{H} = \hbar\omega\left(\hat{N} + \frac{1}{2}\right) \end{align}

0.17.4 Eigenstates of Number Operator

As the number operator \hat{N} is Hermitian, we can find an orthonormal basis \{\Psi_0(x), \Psi_1(x), \ldots\} such that

\hat{N}\Psi_n(x) = E_n\Psi_n(x)

We next prove that E_n can only be non-negative integers.

Given \Psi_n an eigenvector of \hat{N} with eigenvalue E_n, we have

\begin{align} \hat{N}\hat{a}\Psi_n &= \hat{a}^\dagger\hat{a}^2\Psi_n \\ &= (\hat{a}\hat{a}^\dagger - 1)\hat{a}\Psi_n \\ &= \hat{a}\hat{N} - \hat{a}\Psi_n \\ &= (E_n-1)\hat{a}\Psi_n \\ \end{align}

Thus, if \hat{a}\Psi_n is non-zero, then \hat{a}\Psi_n is also an eigenvector of \hat{N} with eigenvalue E_n-1.

We next prove that \hat{a}\Psi_n = 0 if and only if E_n = 0.

If E_n = 0, then

\begin{align} \left<\hat{a}\Psi_n|\hat{a}\Psi_n\right> &= \left<\Psi_n|\hat{a}^\dagger\hat{a}\Psi_n\right> \\ &= \left<\Psi_n|0\right> \\ &= 0 \end{align}

Thus, \hat{a}\Psi_n = 0.

If \hat{a}\Psi_n = 0, then

\begin{align} \left<\hat{a}\Psi_n|\hat{a}\Psi_n\right> &= \left<\Psi_n|\hat{a}^\dagger\hat{a}\Psi_n\right> \\ &= \left<\Psi_n|\hat{N}\Psi_n\right> \\ &= E_n\left<\Psi_n|\Psi_n\right> \\ &= 0 \end{align}

Thus, E_n = 0.

By proceeding the previous argument, we conclude that \hat{a}^k\Psi_n is an eigenvector of \hat{N} with eigenvalue E_n-k.

If En is not an integer, then k can be any positive integer as the annihilation process can be repeated indefinitely when E_n - k never hit zero. And there exits k such that E_n - k < 0, which is not possible, as \hat{N} = \hat{a}^\dagger\hat{a}, and is positive semi-definite.

Thus, E_n is a non-negative integer.

0.17.5 Ground State of Quantum Harmonic Oscillator

By discussion in the previous section, we can find an normalised eigenstate \Psi_0(x) of the number operator \hat{N} with eigenvalue E_0 = 0.

In this section, we prove that it is unique, up to a complex constant.

By previous discussion, we see that \hat{a}\Psi_0 = 0.

\begin{align} u\hat{x}\Psi_0 + v\hat{p} i \Psi_0 &= 0 \\ u\hat{x}\Psi_0 + v\hbar \frac{d}{dx}\Psi_0 &= 0 \\ \end{align}

As the above equation is a first oder homogeneous ODE, and the solution is unique up to a complex constant.

0.17.6 Creation Operator and Eigenstates of Number Operator

Given the ground state \Psi_0(x) of the quantum harmonic oscillator, and eigenstate \Psi_n(x) of the number operator \hat{N} with eigenvalue E_n = n. Then:

\hat{N}\hat{a}^\dagger\Psi_n = (E_n+1) \hat{a}^\dagger\Psi_n

and

\begin{align} \left<\hat{a}^\dagger\Psi_n|\hat{a}^\dagger\Psi_n\right> &= \left<\Psi_n|\hat{a}\hat{a}^\dagger\Psi_n\right> \\ &= \left<\Psi_n|[\hat{a},\hat{a}^\dagger]+\hat{a}^\dagger\hat{a}\Psi_n\right> \\ &= \left<\Psi_n|\Psi_n\right> + \left<\Psi_n|\hat{N}\Psi_n\right> \\ &= E_n + 1 \end{align}

Thus, we could define the recursive relation:

\Psi_{n+1} = \frac{\hat{a}^\dagger\Psi_n}{\sqrt{E_n+1}}

Repeating the formula, we can get all the eigenstates of the number operator \hat{N}. And could be defined by the ground state \Psi_0(x).

\Psi_n(x) = \frac{(\hat{a}^\dagger)^n\Psi_0(x)}{\sqrt{n!}}

0.17.7 Statistics of Quantum Harmonic Oscillator

As the creation operator \hat{a}^\dagger and annihilation operator \hat{a} are linear combinations of position operator \hat{x} and momentum operator \hat{p}, we can derive the position operator \hat{x} and momentum operator \hat{p} in terms of \hat{a} and \hat{a}^\dagger.

\begin{align} \hat{x} &= \frac{1}{\sqrt{2m\hbar\omega}}(\hat{a} + \hat{a}^\dagger) \\ \hat{p} &= \frac{i}{\sqrt{2m\hbar\omega}}(\hat{a} - \hat{a}^\dagger) \end{align}

Thus, we have

\begin{align} \left<\Psi_n|\hat{x}\Psi_n\right> &= \frac{1}{\sqrt{2m\hbar\omega}}\left<\Psi_n|(\hat{a} + \hat{a}^\dagger)\Psi_n\right> = 0 \\ \end{align}

and

\begin{align} \left<\Psi_n|\hat{p}\Psi_n\right> &= \frac{i}{\sqrt{2m\hbar\omega}}\left<\Psi_n|(\hat{a} - \hat{a}^\dagger)\Psi_n\right> = 0 \\ \end{align}

0.18 Constant of Motion and Commutators

Given an operator \hat{A}, which is probably time dependent, then

\begin{align} \frac{d}{dt}\left<A\right> &= \frac{d}{dt}\left<\Psi|\hat{A}\Psi\right> \\ &= \frac{d}{dt} \int_{-\infty}^{\infty} \Psi^*\hat{A}\Psi dx \\ &= \int_{-\infty}^{\infty} \left(\frac{\partial \Psi^*}{\partial t}\hat{A}\Psi + \Psi^*\frac{\partial \hat{A}}{\partial t}\Psi + \Psi^*\hat{A}\frac{\partial \Psi}{\partial t}\right) dx \\ &= \left<\Psi|\frac{\partial \hat{A}}{\partial t}\Psi\right> +\int_{-\infty}^{\infty} \left(\frac{\partial \Psi^*}{\partial t}\hat{A}\Psi + \Psi^*\hat{A}\frac{\partial \Psi}{\partial t}\right) dx \\ &= \left<\Psi|\frac{\partial \hat{A}}{\partial t}\Psi\right> + \left<\frac{\partial \Psi}{\partial t}|\hat{A}\Psi\right> + \left<\Psi|\hat{A}\frac{\partial \Psi}{\partial t}\right> \\ &= \left<\Psi|\frac{\partial \hat{A}}{\partial t}\Psi\right> + \left<\left(\frac{1}{i\hbar}\hat{H}\Psi\right)|\hat{A}\Psi\right> + \left<\Psi|\hat{A}\left(\frac{1}{i\hbar}\hat{H}\Psi\right)\right> \\ &= \left<\Psi|\frac{\partial \hat{A}}{\partial t}\Psi\right> + \frac{1}{i\hbar}\left[ - \left<\Psi|\hat{H}\hat{A}\Psi\right> + \left<\Psi|\hat{A}\hat{H}\Psi\right> \right] \\ &= \left<\Psi|\frac{\partial \hat{A}}{\partial t}\Psi\right> + \frac{1}{i\hbar} \left<[\hat{A},\hat{H}]\right> \end{align}
←Previous PostNext Post→